305 Million Solutions to The Black-Scholes Equation in 16 Minutes with AWS Lambda

Originally Posted: May 28, 2017

The research I’m working on involves estimating a firm’s probability of default over a variety of time horizons using the Merton Distance to Default model. The dataset contains daily financial information for more than 24,000 firms over the past 30 years. Given that I am calculating the probability of default over five time horizons, applying the Merton model will require solving the Black-Scholes equation roughly 305 million times. Luckily, the model is easily parallelized because the only data needed for the model, aside from the risk-free rate, is firm specific. This post shows how the Python library Pywren can leverage AWS Lambda to run hundreds of models in parallel, achieving a 270x speed-up over a quad-core i7-4770, with minimal changes to the simulation code. If you are interested in learning more about the model, see my post about implementing the model in Python.

Define The Function to Run on Lambda

Depending on what you need to solve, you may be able to pass information directly to Lambda via Pywren’s interface. My data was stored in S3 already, so I wrote a function that takes an S3 key and then handles loading the data, running the simulation, and writing the results to S3. The full code is available on my Github repo, but the main function of interest is:

def run_model(key, time_horizon=[1,2,3,4,5]):
    '''
    Apply B-S option pricing model to calculate inferred firm asset values as a
    function of time.

    Args:
        key (str): key pointing to data in S3
        time_horizon (list): List of time horizons (In Years) to calculate model over

    Returns:
        float: Time run was started (In unix time)
        float: Time run finished (In unix time)
        dict: Response from S3 write
    '''
    start = time.time()

    # Get data from S3
    h_map, dates, data = get_data(key)

    # Check if there is at least one year's worth of historical data
    if len(dates) > 252:
        # Run the simulation
        results = solve_for_asset_value(data, h_map, time_horizon=time_horizon)

        # Merge data back into CSV
        csv_file = merge_data_to_csv(h_map, dates, data, results)

        # Save results to S3
        result_key = key.replace('merged-corp-data', 'merton-results')
        response = save_data(csv_file, result_key)
    else:
        response = False

    end = time.time()

    return start, end, response

Executing on Lambda

Pywren makes executing your function on Lambda incredibly easy and familiar to anyone that has used Python’s map function or Python’s process pools. Behind the scenes, Pywren handles serializing all the supporting functions, data, etc. that are needed to execute your code on Lambda. This is what it comes down to:

import pywren

# Create a Pywren executer
wrenexec = pywren.default_executor()

# Use the executer's map function just like Python's map
futures = wrenexec.map(run_model, bucket_contents)

# Get the results
map_results = pywren.get_all_results(futures)

Figure 1 below shows that within about 15 seconds of execution, the number of workers ramps up to a peak of ~900 and holds steady for ~16 minutes until execution finishes. The shaded gray lines show the runtime of each individual job.

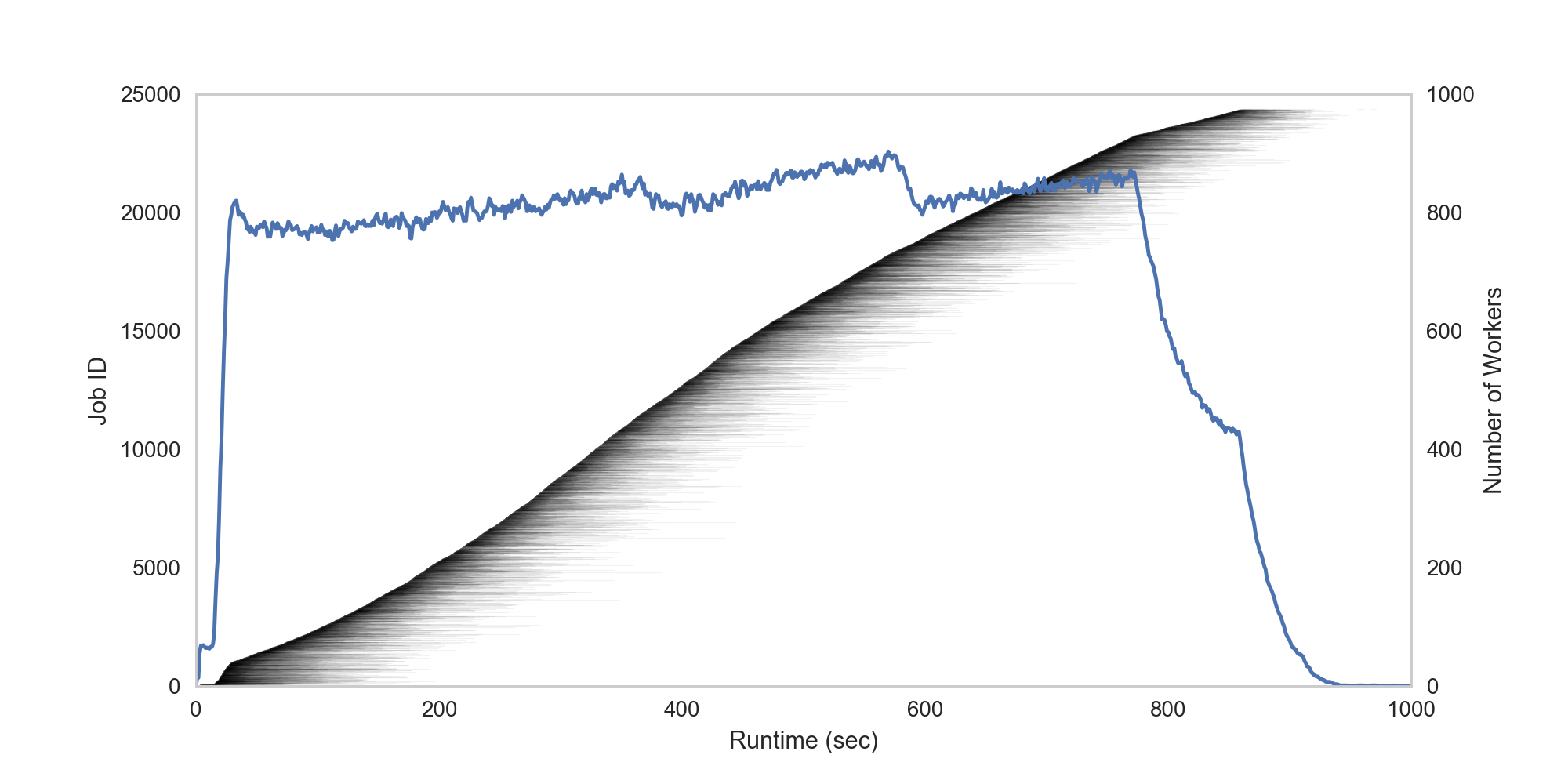
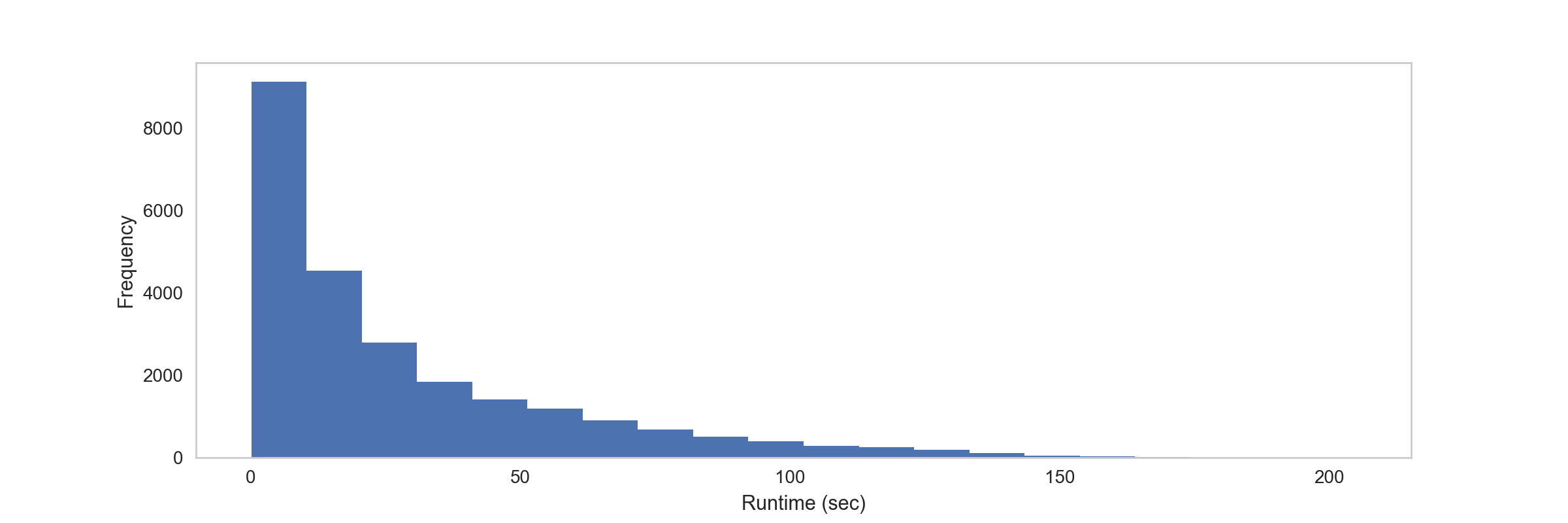
Figure 2 shows that the majority of the simulation runs take less than 60 seconds to complete, well under Lambda’s time limit of 300 seconds:

Conclusion

Pywren makes it incredibly easy to leverage AWS Lambda for compute tasks, especially tasks which are inherently easy to parallelize. For more details on the exact performance that can be harnessed from Lambda, see the benchmarking done by Pywren’s authors, Eric Jonas et al.