Bradford (Lynch) Levy

✅💯 Booth RP 2023 Interviewing: Set up for success

Originally Posted: May 07, 2023

This post is meant to help “level set” across candidates interviewing for my Research Professional position at Chicago Booth in Summer 2023. Interviews will last 45 minutes, allocated as follows:

🫱‍🫲 Introduction (5 min)
📡 Data collection (15 min)
📊 Data processing (15 min)
🧐 Interviewee questions (10 min)

The goal of the interview is to assess your ability to think through a problem and develop a solution. While it is great if you can write functional code in real-time, that is not necessarily expected. To that end, focus on the problem itself and conveying how you are thinking about it, possible solutions, and the pros and cons associated with the solutions you envisage. Thinking out loud is great!

Continue reading to learn about setting yourself up for success during the interview.

Originally Posted: June 30, 2022

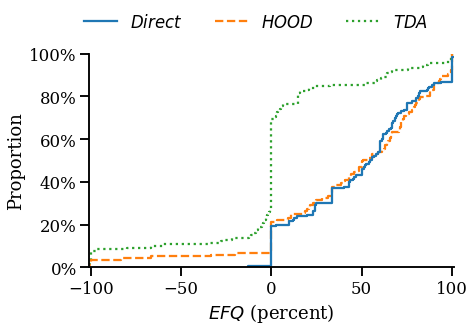
Figure 1. Execution Quality Across Brokers

In a new study, I use a randomized controlled trial to examine the effect of payment for order flow (PFOF) on price improvement (PI). The results suggest the national best bid and offer overstates PI by as much as 400%, and that PFOF can benefit investors, but significant heterogeneity exists across brokers. The results highlight important policy implications, specifically the need for better measures of market conditions, execution quality disclosures, and a more precise definition of “best execution.”

Along these lines, the SEC cited this work in December 2022 proposals which would amend Regulation National Market System (Reg NMS) with the goal of increasing competition and new rules governing best execution—changes which have been regarded as “biggest shakeup to stock market rules since the SEC introduced Regulation National Market System in 2005[.]”

Originally Posted: January 01, 2018

In this post, I show that search-based identification of peer firms yields groups which transcend traditional industry classification codes and use stock return data to show that they are more economically related. This indicates that investors may be better off using more novel means of finding comparable companies than relying solely on traditional Standard Industrial Classification (SIC) codes. Building upon my last post, SEC Filings Graph, which explored logs from one year of searches on the SEC’s EDGAR website to identify related companies, I expand the data to searches from January 2008 through March 2017 and implement quantative measures of economic relatedness between the firms within a peer group. The resulting dataset (previous dataset) has 407,574,804 (52,611,188) searches for 9,583,773 (5,388,574) reports by 3,043,255 (476,827) users. My work is inspired by, and roughly follows, the methodology of Lee et al. who studied search data for 2008 through 2011.

Originally Posted: November 26, 2017

Graphs let us model the world as it is, with nodes that represent physical entities and edges connecting nodes based on the relationships between them. Inspired by the work of Lee et al., I took the Thanksgiving weekend to build a graph of SEC filings. In this post, I use the EDGAR Log File Dataset, from April 2016 through March 2017, and Neo4j to build a graph of 52,611,188 searches for 5,388,574 reports by 476,827 users. The graph leads to interesting connections between firms and could be extended to include more relationships and entities from other domains such as textual similarity of filings, employment histories of material employees, and patent applications.

Originally Posted: May 28, 2017

The research I’m working on involves estimating a firm’s probability of default over a variety of time horizons using the Merton Distance to Default model. The dataset contains daily financial information for more than 24,000 firms over the past 30 years. Given that I am calculating the probability of default over five time horizons, applying the Merton model will require solving the Black-Scholes equation roughly 305 million times. Luckily, the model is easily parallelized because the only data needed for the model, aside from the risk-free rate, is firm specific. This post shows how the Python library Pywren can leverage AWS Lambda to run hundreds of models in parallel, achieving a 270x speed-up over a quad-core i7-4770, with minimal changes to the simulation code. If you are interested in learning more about the model, see my post about implementing the model in Python.

Originally Posted: May 20, 2017

One of the most effective methods for rating credit risk is built on the Merton Distance to Default model, also known as simply the Merton Model. While implementing this for some research, I was disappointed by the amount of information and formal implementations of the model readily available on the internet given how ubiquitous the model is. This post walks through the model and an implementation in Python that makes use of Numpy and Scipy.

Originally Posted: March 02, 2016

One challenge facing companies that manufacture products with highly seasonal demand is the choice of production scheduling. One option is to make a fraction of the expected demand each month leading up to the peak season. But, when demand is uncertain this approach can lead to large overages or shortages that erode margins. Firms that find themselves in this situation must balance the costs of ramping production to meet demand during peak season, additional inventory holding costs, and the risk of uncertain demand.

The case of Play Time Toy Company¹ is used to explore solutions to this dilemma. Specifically, using Monte Carlo analysis to assess the impact of production scheduling on firm profitability and capital requirements.

Originally Posted: December 08, 2015

This post examines how the formal structure set by managers can differ drastically from its informal structure which dictates how information flows within the company.

Originally Posted: December 04, 2015

The need to make trade-offs between the effort exerted on specific activities is felt universally by individuals, organizations, and nations. In many cases, activities are mutally-exclusive so partaking in one option excludes participation in another. Deciding how to make these trade-offs can be immensely difficult, especially when we lack quantitative data about risk and reward to support our decision.

In the case of financial assets, there is a wealth of numerical data available. So in this post, I explore how historical data can be leveraged to choose specific mixes of assets based on investment goals. The tools used are quite simple and rely on the mean-variance of assets’ returns to find the efficient frontier of a portfolio.

Note: The code and data used to generate the plots in this post are available here.

Originally Posted: October 12, 2015

Gearing on a bicycle enables the rider to traverse differing terrain while maintaining a comfortable pedaling speed, known as “Cadence”, and road speed. For instance, a cyclist with just one gear, riding on flat terrain at 20 mph and pedaling at 90 RPM would have to slow their pedaling speed to just 45 RPM while riding uphill at 10 MPH. Not only is pedaling at 45 RPM going uphill difficult, it also puts excessive stress on the rider’s body and is inefficient; most people’s optimal pedaling speed is 90RPM (Neptune, Journal of Biomechanics 409-415). Thus, it is desirable to have a set of gear ratios to use while traversing varying terrain.

The race for market share in the world of cycling while trying to meet this need has driven growth from bicycles with 10 speeds in 1983 to cycles with 20+ speeds in 2015. This level of gearing requires narrower chains and higher precision shifting mechanisms, thus adding cost and complexity to the machines. It is interesting to note that while the number of gears on a racing bike has steadily increased, the gearing range hasn’t. This has resulted in redundant gear ratios throughout the available range on most bikes. New drivetrains are now placing an emphasis on simplicity by including fewer gears in total while providing a similar number of unique gear ratios. To understand how many gears are truly needed, the author analyzed gear usage during rides on a variety of terrain.